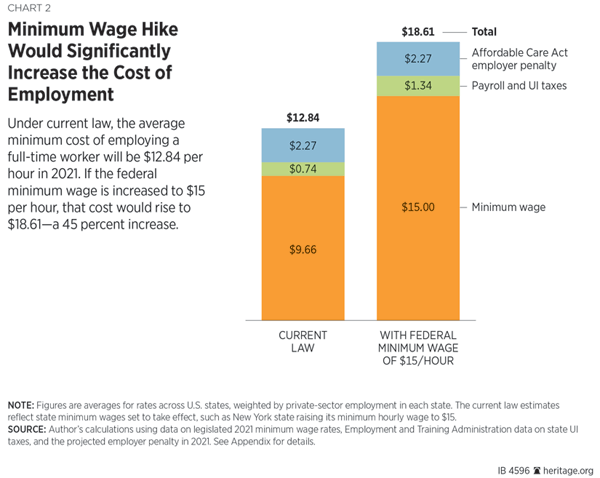Prominent Members of Congress have proposed raising the minimum wage to $15 per hour, more than doubling the federal minimum wage. States with lower costs of living would see an even greater real increase. At the state level, the minimum wage would cover one-third of wage and salary workers. The new minimum-wage legislation, including payroll taxes and the employer mandate, would increase the minimum cost of hiring a full-time worker to $18.61 per hour.
Businesses would respond to these higher labor costs by reducing employment of affected workers by over one-sixth, thus eliminating approximately seven million full-time-equivalent (FTE) jobs by 2021. Forcing employers to pay starting wages of $15 per hour would make many less skilled workers unemployable.
Growing Support for $15-an-Hour Starting Wages
A $15-per-hour minimum wage was once a fringe idea. Politicians of every ideological stripe agreed that raising starting wages that high would eliminate too many job opportunities. Nonetheless, recent, union-backed campaigns have pushed the idea into the mainstream.
The California and New York legislatures recently passed bills raising minimum starting wages in their states to this level.[1] Several cities, including Washington, DC, have also passed $15-per-hour minimum wages.
In Congress, Senator Bernie Sanders (I–VT) has introduced the Pay Workers a Living Wage Act, which would raise the federal minimum wage from $7.25 per hour to $15.00 per hour over four years.[2] Prominent Senators, including Assistant Minority Leader Dick Durbin (D–IL), have co-sponsored this bill. The Democratic Party has formally included a $15-per-hour minimum starting wage in its 2016 campaign platform.[3]
Since the $15-per-hour minimum wage was a fringe proposal, it received relatively little empirical examination. Economists widely agreed $15 was too high, and instead examined smaller increases that actually had political support. This Issue Brief fills that gap, examining how a $15-per-hour federal minimum wage would affect workers.
Unprecedented Increase
If Congress passed the Pay Workers a Living Wage Act in 2017, the federal minimum wage would rise to $15 by 2021 (equal to $13.80 in 2016 dollars).[4] In contrast, adjusted for inflation, the federal minimum wage has never stood higher than $8.55 per hour.[5] No state has increased starting wages above $10.00 per hour. (The California and New York increases have not yet taken full effect.)[6] Raising minimum starting wages this high has no historical precedent.
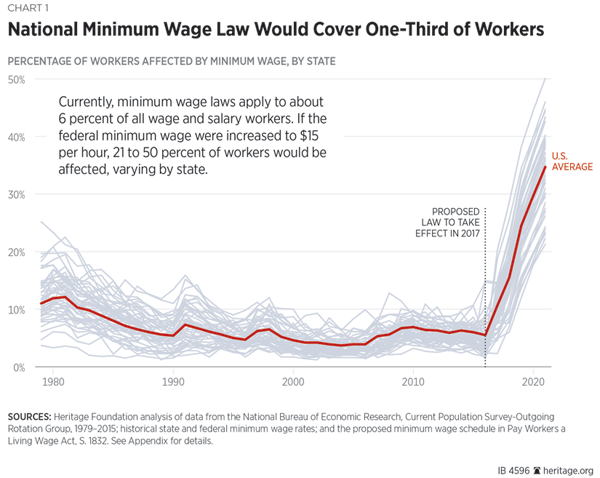
Table 1 shows how raising the federal minimum wage to $15 per hour in 2021 would directly affect one-third of wage and salary workers (44.9 million employees).[7] Lower-wage jobs are more likely to be part-time than higher-wage positions, so the increase would affect a somewhat smaller proportion (28.2 percent) of total hours worked in the economy. Those work hours still represent 37.5 million FTE jobs.[8] These numbers do not include “spillover effects” from near-minimum-wage employees getting raises to maintain pay differentials.
At the $15-per-hour level, minimum starting wages would affect a greater proportion of workers than ever before. Chart 1 shows the proportion of workers directly affected by the minimum wage by state and year, along with average coverage across the U.S.[9] Federal and state minimum wages typically cover between 4 percent and 10 percent of the workforce. At present, 5.5 percent of workers across the U.S. make the minimum starting wage. In the late 1970s and early 1980s, the federal minimum wage briefly covered as many as one in five workers in some Southern states with low costs of living (Mississippi, Arkansas, and Alabama).
Chart 1 also shows how raising the minimum wage to $15 per hour using the schedule proposed by Senator Sanders would bring it to cover one-third of the workforce.[10] The minimum wage has never before come close to covering such a large share of workers. Whether expressed in real dollars or as a proportion of workers directly affected, no state has experienced minimum starting wages this high.
Larger Impact in Areas with Lower Living Costs
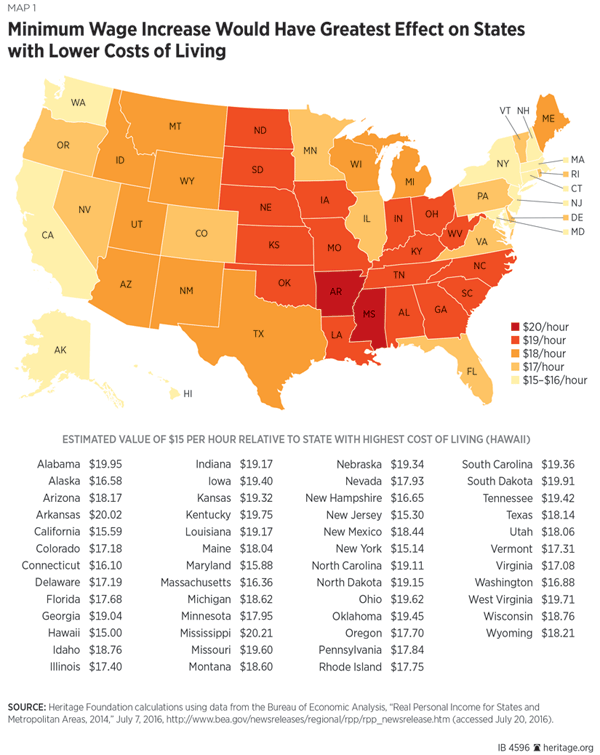
A $15 federal mandate would have a greater effect in states with lower costs of living. Employers in lower-cost areas generally pay lower wages, although those wages purchase more goods and services than they would in high-cost areas.[11] The federal minimum wage ignores these regional living cost differences. Thus, employers in Mississippi or Ohio would have to pay the same starting wages as employers in California or New York—even though those wages purchase considerably more goods and services in low-cost areas.
A federal minimum-wage increase disproportionately affects states with lower living costs. Map 1 shows the value of $15 per hour, relative to living costs in the state with the highest living costs (Hawaii). As the map illustrates, living cost differences considerably affect effective wages. A minimum starting wage of $15 per hour has similar purchasing power in high-cost states like Hawaii, New York, and California. However, it would take approximately $20 per hour in Hawaii to purchase the same goods and services that $15 per hour buys in low-cost states like South Dakota, Arkansas, or Alabama.
Employer Costs Would Rise Above $15
Raising minimum starting wages to $15 per hour would actually raise hiring costs well above $15 per hour. The Affordable Care Act (Obamacare) requires most employers with 50 or more employees to offer full-time workers qualifying health coverage.[12] Failing that, they must pay a per employee penalty (after the first 30 workers) out of after-tax dollars.[13] The penalty currently stands at $2,160 per employee and is projected to rise to $2,886 by 2021.[14] This equates to a $4,731 increase in pre-tax payroll costs[15]—$2.27 per hour for a full-time worker.[16]
These costs come on top of other government mandates. Businesses must also pay the employer share of payroll taxes and unemployment insurance (UI) taxes. Businesses normally defray these costs by reducing workers’ wages by an offsetting amount. However, employers cannot reduce the pay of minimum-wage employees, so they must pay these payroll costs themselves or forgo hiring.
Chart 2 shows the minimum costs of hiring a full-time worker in 2021 under current federal and state laws. Under current law minimum hiring costs will stand at $12.84 per hour.[17] This includes the effect of states like California and New York raising their minimum wage, as well as payroll and UI taxes and the Obamacare mandate.
If Congress raises the federal minimum wage to $15 per hour, minimum hiring costs will rise to $18.61 per hour. That figure includes:
- $15.00 for the minimum wage,
- $0.19 in unemployment insurance taxes,
- $1.15 in payroll taxes, and
- $2.27 per hour in Obamacare penalties.
Government mandates add at least $3.61 to employers’ full-time hiring costs, although employees do not see those costs in their paychecks.
Hurting Less Skilled Workers
Raising minimum starting wages to $15.00 would badly hurt many workers. Companies hire workers when the additional earnings their labor creates exceeds the cost of employing them. Starting wages of $15.00 per hour mean full-time employees must create at least $38,700 a year in value for their employers. Such a high hurdle would make it much harder for less experienced and less skilled workers to find full-time jobs. Many of these workers are not yet productive enough to create that much value for their employers, and businesses will not hire them at a loss.
Moreover, Senator Sander’s legislation does not establish lower starting wages for youth; it covers everyone irrespective of age. This lack of distinction would make it particularly difficult for younger workers to find entry-level jobs. Most teenagers lack the skills necessary to produce over $15 per hour in additional earnings for their employer.[18]
Even Liberal Economists Agree $15-an-Hour Mandate Hurts Workers
Raising starting wages to $15 per hour has gained political support. However, even liberal economists widely agree it would hurt workers. Princeton economist Alan Krueger, the former Chair of President Obama’s Council of Economic Advisers, explained that “a $15-per-hour national minimum wage would put us in uncharted waters, and risk undesirable and unintended consequences…. [T]he push for a nationwide $15 minimum wage strikes me as a risk not worth taking.”[19]
Harry Holzer, a senior researcher affiliated with both the Brookings Institution and the Urban Institute, who previously served as the chief economist in the Labor Department under President Clinton, also opposes a $15 minimum wage:
[S]uch increases are extremely risky. In job markets where young or less-educated workers already have difficulty finding jobs and gaining important work experience, such mandates will likely make it much harder…. Many employers will be very reluctant to pay high wages to workers whose skills—including the ability to speak English, in the case of many immigrants—are so modest.[20]
These views appear widespread among liberal economists, although many have kept quiet about their reservations. Dylan Matthews, a writer for the liberal news site Vox.com, recently wrote he had observed “[o]ne really fascinating phenomenon: left-wing economists saying off the record that $15/hr is super-dangerous, but not saying that publicly.”[21]
Wage Mandates Eliminate Jobs
Economists have good reason for these reservations. If Congress passed a $15 federal minimum wage, employers would have to increase affected workers’ wages by an average of 27.4 percent.[22] Additional raises are likely for workers currently making near $15 per hour.[23] Quantifying the magnitude of these “spillover” effects, however, is highly subjective.[24] Wages will almost certainly increase more than the minimum necessary to comply with the law, but predicting how much more is difficult.
Increasing starting wages to $15 per hour would eliminate jobs and reduce hiring. When a good or service becomes more expensive, consumers buy less of it. Employers react the same way when wages rise. If Congress raised minimum starting wages to $15—and total hiring costs to $18.61 per hour—businesses would respond by eliminating positions, cutting hours, and looking for new ways to implement labor-saving technology. Some companies might have to face shutting down or leaving America entirely to cope with the additional expenses.
In fact, that process has already begun in California. Shortly after Los Angeles raised its minimum wage to $15 per hour, American Apparel eliminated 500 clothing manufacturing jobs in the city. The Los Angeles Times reports the company planned to relocate those jobs within California. After California raised minimum starting wages statewide, however, American Apparel began examining options to move production outside California.[25]
Seven Million Jobs Lost
Existing minimum-wage studies shed little light on the total number of jobs a $15 mandate would cost. Those studies examined much smaller minimum-wage increases that affected relatively few workers. Most of these studies look at just teenage employment or the restaurant sector—the only sectors significantly impacted by the increase. They provide little guidance on the effects of a minimum wage covering one-third of the workforce.
However, economists have extensively studied how businesses respond to higher wages overall, not just minimum-wage increases.[26] On average these studies find a 10 percent increase in labor costs causes firms to reduce employment of less-skilled workers by 6.8 percent in the long run.[27] This is not a precise estimate—some studies find greater job losses, others find lower. This average does indicate, however, the approximate magnitude of job losses that occur when labor costs rise.
These studies imply that if Congress raised starting wages to $15 employers would reduce employment of affected workers by approximately 19 percent.[28] That represents about 6.9 million fewer FTE jobs in the U.S. by 2021.[29] These job losses come on top of jobs lost by state-level minimum-wage increases. The Pay Americans a Living Wage Act would prevent seven million workers from getting paid anything.
Conclusion
Raising minimum wages to $15 per hour has quickly gone from a fringe idea to a serious policy proposal. Such an increase would bring the federal minimum wage into uncharted territory. At that level, the minimum wage would cover one-third of the U.S. workforce—37.5 million FTE jobs. The increase would have particularly large effects on states with lower costs of living. Including the cost of mandatory employer taxes, minimum hiring costs for a full-time worker would rise to $18.61 per hour.
Such a large increase in starting wages would make it difficult for less skilled workers to find jobs. Employers will not pay workers more than the value they produce. Employers would respond by reducing employment of affected workers by approximately one-fifth, eliminating roughly seven million FTE jobs.
—James Sherk is Research Fellow in Labor Economics in the Center for Data Analysis, of the Institute for Economic Freedom and Opportunity, at The Heritage Foundation.
Appendix
Table 1
The figures in Table 1 were calculated using Current Population Survey–Outgoing Rotation Group data from the National Bureau of Economic Research.[30] Hourly earnings for workers in the CPS–ORG data were calculated using the reported hourly wage of hourly workers, and dividing usual weekly earnings by usual hours worked for salaried workers. Hourly earnings of waiters in bars and restaurants were calculated using the same method as for salaried workers.[31] The author excluded imputed observations, as well as respondents with calculated hourly earnings below $1 per hour or above $200 per hour.[32]
CPS–ORG data show that between 2007 and 2015 median nominal wages for adult (25–59-year-old) workers in the U.S. grew 1.68 percent a year. The author used this inflation factor to convert $15 per hour in 2021 into 2015 dollars ($13.57 per hour).[33]
Estimated hourly earnings were then adjusted for future minimum-wage increases. Many states have legislated minimum-wage hikes that will take place over time, such as California and New York’s phased-in $15 mandates. To account for this, the author calculated nominal minimum wages in each state in 2021.[34] The author used the 1.68 percent inflation factor to convert these nominal 2021 minimum-wage values into 2015 dollars. Reported hourly earnings for any worker in the 2015 CPS–ORG reporting less than their state’s 2021 minimum wage (in 2015 dollars) were replaced with the mandated minimum wage.
Table 1 displays the proportion of wage and salary workers in the 2015 CPS–ORG whose adjusted earnings are less than $13.57 per hour ($15 in 2021 dollars). This figure is 33.1 percent. This calculation treats agricultural workers as unaffected by the increase as the federal minimum wage does not cover them, and entirely excludes self-employed workers for the same reason. Any worker in a state with a minimum wage at $15 per hour in 2021 (i.e., New York) is treated as unaffected as their adjusted earnings already stood at $13.57 per hour. The same calculation was performed, weighting by hours worked, to estimate the total proportion of wage and salary work hours directly affected by a $15-per-hour federal minimum wage: 28.2 percent.
To estimate the number of workers affected, the author projected U.S. employment in 2021. Between 2010 and the June 2016 payroll survey, employment grew an average of 1.39 percent a year. In June 2016, the payroll survey reported 151.1 million Americans had jobs. The author extrapolated that growth rate forward to estimate total U.S. employment of 161.9 million in 2021.
This estimate includes self-employed Americans not covered by the minimum wage. The calculations reported in Table 1 were re-estimated for all workers, including the self-employed. These calculations showed that a $15 federal minimum wage in 2021 would affect 27.7 percent of all workers (including minimum-wage-exempt self-employed workers). Those workers work 24.1 percent of all hours in the economy. The author multiplied the 27.7 percent estimate by 161.9 million total workers in 2021 to estimate a federal increase would affect 44.9 million workers.
To estimate the number of FTE jobs lost the author calculated the ratio of FTE workers to total workers in the 2015 CPS–ORG: 96.0 percent.[35] The author multiplied that ratio by estimated 2021 total employment to estimate the U.S. economy will have 155.5 million FTE workers in 2021. This figure includes self-employed workers. This figure was multiplied by the 24.1 percent of all work hours (affected including self-employed hours) to conclude a $15 federal mandate would affect 37.5 million FTE jobs.
The author also calculated the average amount affected workers’ adjusted base earnings (as described above) would have to rise to reach $13.57 per hour in the 2015 CPS–ORG. Weighted by hours worked this figure was 27.4 percent. This figure is net of future state minimum-wage increases. For example, California will have a $14-per-hour minimum wage in 2021. It will thus take a relatively smaller increase for California employers to come into compliance than employers in other states. The figure presented in Table 1 takes account of this fact and only shows the incremental effect of a federal increase, above and beyond already legislated state increases.
6.9 Million Jobs Lost
In their Appendix Table B-3 Lichter et al. (2009) report meta-regression estimates of the own-wage elasticity of labor demand that account for publication bias. The coefficients on these estimates imply an elasticity of –0.677 for a study published in 2012 (the most recent year in their data) of long-run unconditional labor demand for low-skilled labor in the U.S., estimated using industry-level administrative panel data and a structural form model.[36]
Multiplying this long-run elasticity by the 27.4 percent wage increase necessary to comply with a $15 mandate shows employers would reduce total labor demanded by –0.677 * 0.274 = 18.5 percent.[37] That figure, multiplied by 37.5 million FTE jobs shows the Pay Americans a Living Wage Act would cause employers to eliminate approximately 6.9 million FTE jobs. These losses would take the form both of hour reductions and jobs lost. These figures represent the incremental effect of a federal increase over and above existing state minimum-wage increases.
Chart 1
The author calculated Chart 1 using data on historical state minimum-wage rates and the 1979–2015 CPS–ORG. Hourly earnings were calculated as described for Table 1. For each year from 1979 to 2015, the author calculated the proportion of workers in each state making less than their state or federal minimum wage (whichever was binding).
Chart 1 also displays the average percent of workers directly covered by the minimum wage across all states. For 2016, the author used 2015 CPS–ORG data, but calculated nominal 2016 minimum wages in 2015 dollars (using the 1.68 percent inflation factor).
For 2017 to 2021 the analysis uses the minimum-wage schedule set out in the Pay Workers a Living Wage Act, assuming Congress passed it in 2017, or the relevant state minimum wage (whichever was greater). These figures are converted into 2015 dollars and calculated using the 2015 CPS–ORG.
Map 1
Map 1 converts $15 per hour nationally into living cost adjusted dollars that account for price differences across states. These relative wages are expressed relative to Hawaii, the state with the highest living cost in 2014. The author did this by dividing $15 by the ratio of the Bureau of Economic Analysis’ estimate of each state’s regional price parity (RPP) value for all goods and services in 2014 and the RPP for all goods and services for Hawaii that year.
For example, Indiana had an RPP of 91.4 in 2014 while Hawaii’s was 116.8. The author divided $15 by (91.4/116.8) to estimate a relative minimum wage of $18.17 per hour in Indiana. This means that $15 has the same purchasing power in Indiana that $18.17 does in Hawaii.
An alternative measure of living costs comes from the Council for Community and Economic Research (C2ER). This report used RPP data instead of C2ER data for two reasons:
- C2ER living-cost comparisons measure the prices of goods and services purchased by professional and managerial households in the top income quintile. They do not examine consumption baskets purchased by lower-income workers.
- C2ER data measures housing costs by comparing new home purchase prices across cities. The RPP measures housing costs by comparing rental prices. Research finds that wages track living costs estimated using rental values much more closely than living costs estimated using home purchase prices.[38]
Chart 2
The author calculated the minimum cost of hiring a full-time, full-year employee in each state in 2021 assuming no increase in the federal minimum wage but that state minimum wages take effect as currently legislated. For each state, the author took the legislated minimum wage in 2021 and added to it the 7.65 percent share of employer payroll taxes. Minimum wages indexed to inflation were calculated assuming 1.68 percent inflation each year indexing occurs.
To these amounts were added the prorated hourly cost of the Obamacare penalty ($2.27 per hour) and the prorated hourly cost of UI taxes paid by a newly formed business hiring a full-time worker at the minimum wage in that state.
In states for which UI tax rates for new firms are calculated separately by industry, the average employer rate for the entire state was used. These proration calculations assumed a full-time worker puts in 2,080 hours a year. The national average was then calculated by taking the weighted average of these state-specific hourly costs, with the weights being each state’s share of total employment between June 2015 and May 2016.
Calculating minimum hiring costs under a federal minimum wage of $15 per hour proceeded as above, except that every state was assigned a $15.00-per-hour minimum wage. In these calculations the only differences between state hiring costs come from differences in UI tax rates and UI taxable wage bases.
This employer penalty is linked to the growth of health care premiums. Mercer LLC projects the employer penalty will rise to $2,260 in 2017. This report projects the average annual growth rate between 2017’s estimated penalty and the 2015 penalty forward to 2021.[39] Under these assumptions, the penalty will stand at $2,886 in 2021. In pre-tax dollars that amounts to $4,731, which prorates out to $2.27 per hour over 2,080 hours a year.