Economic analysis of climate change and climate policies is fraught with many problems. Uncertainty and imprecision surround fundamental scientific and economic factors, such as, for example, how much warming will result from a doubling of carbon-dioxide (CO2) levels and how much damage is done by a given change in average world temperature. This paper addresses the following question: How does economic analysis compare costs and benefits when they occur at different times?
In a broad sense, this question can be addressed by looking at climate policy as an investment. Investment requires giving up something now and receiving something in the future. An investment that will generate less than its initial cost makes little sense. Though investment opportunities are virtually unlimited, there are limited resources for undertaking them, so not all investments that pay more than their costs are worth undertaking.
Any particular investment should be undertaken only so long as it does not crowd out a superior investment. In practice, this standard is tested by comparing an investment’s rate of return to a comparable market rate of interest. The tool for performing this test is discounting. Discounting is compounding run backwards. The product of discounting is called “present value” or “discounted present value” (henceforth referred to as “present value”). For instance, if $100 left in the bank for two years would be worth $121, then $121 received two years from now would have a present value of $100.
Applying Discounting to Climate Policy
Climate economists use mathematical models to estimate the impact that human emissions of carbon dioxide will have on the climate. The models estimate a range of possible future temperature changes caused by the emissions. These temperature changes are then plugged into different models that attempt to quantify the potential cost of environmental damage (from things like sea-level rise and changing weather patterns) at some future point in time. The point in time chosen is often far in the future, and the projected cost of environmental damage may be quite high.
In general, the payback for cutting CO2 emissions comes with such delay that those making the “investment” now are different from those who will reap the benefits later. Of course, climate policy is not the only investment those in the present can make to provide benefits to those in the future. Discounting allows comparison of this climate investment to a set of alternative investments, with the end goal of finding whatever investment will provide the greatest benefit to its recipients in the future.
Some economists argue that using any positive discount rate is inappropriate.[1] In essence, this argument holds that discounting more heavily weights the welfare of those alive today relative to that of those who are yet to be born and is, therefore, immoral. However, this view is based on a flawed understanding of discounting. The discount rate reflects the value of alternatives to the policy in question. It is not a tool for diminishing relative importance of life or utility in the future.
The following hypothetical example can illustrate the absurdity of denying the use of positive discount rates. Suppose a salesman markets to grandparents an investment fund that will provide college tuition for their grandchildren. The salesman argues that the return on the fund will be zero since it is immoral to weigh a dollar’s benefit for the grandchildren at a value of anything less than a dollar to the grandparents. That is, the grandparents should put $100,000 into the fund today in order to provide tuition of $100,000 two decades later. This sales pitch is as nonsensical as the argument that discounting is immoral. Grandparents can do better for their grandchildren than a zero rate of return. Policymakers can do better as well and should refrain from pursuing zero-rate-of-return policies that arise when discounting is ignored.
How Discounting Works
Which stream of receipts is better, a million dollars per year for 20 years or $21 per year for a million years? To choose the first stream is to use discounting, at least implicitly. Even though simple addition shows the second stream of payments generates an additional million dollars, the reasonable choice is the first stream. Since ten hours’ worth of income from the million-dollars-per-year stream could be invested at a modest rate to replicate the $21-per-year stream of payments, the choice is especially easy.[2]
Not all questions of discounting, however, are so obvious. When the costs and benefits of an investment or a policy occur at different times they need to be compared in a way that accounts for these time differences. The guiding question for the comparison is straightforward: How much would have to be invested today to generate the future value in question?
The three factors needed to calculate a present value are:
- The future value,
- The length of time, and
- The interest or discount rate.
The lower the future value in question, the lower will be its present value. A higher interest (discount) rate or a longer time horizon will also lead to lower present value.
The guiding question can be rephrased as how much money needs to be put into a savings account to generate the future value in question? The higher the interest rate or the longer the time interest accrues and compounds, the less is needed for the initial bank deposit.[3]
The most controversial part of present value calculations for climate impacts is choosing the appropriate discount rate. The case of the Environmental Protection Agency/Interagency Working Group (EPA/IWG)’s estimation of the social cost of carbon (SCC) illustrates the calculation’s high sensitivity to choice of discount rate.[4]
The Office of Management and Budget (OMB) guidance to regulatory agencies stipulates discount rates of 3 percent and 7 percent per year for benefit-cost analysis. The EPA/IWG, however, used rates of 2.5 percent, 3 percent, and 5 percent. The EPA/IWG settled on 3 percent as the best choice, but its omission of 7 percent was glaring to those who follow this regulatory issue. When Heritage Foundation researchers re-ran the models using the 7 percent discount rate, the SCC dropped by more than 80 percent in one of the models and actually went negative in the other.[5]
How Is the Social Cost of Carbon Used by Policymakers?
The SCC is a benchmark to guide policymakers on the optimal or efficient amount of CO2 reduction. It is not intended to compel the elimination of all future climate damage from CO2 emissions. In the world of the economist, all or none is rarely the right answer. Instead their answers revolve around optimal adjustments—giving a little here to get a little more there. The SCC is an exercise in comparison—comparing a monetized cost of today’s action with a monetized future benefit of today’s action.
Some may find it totally illegitimate to express environmental impacts in dollar terms. These policymakers may feel it is illegitimate to compare values from market transactions to changes in sea level or temperature or other environmental changes. For them, social cost of carbon calculations and, perhaps, environmental economics altogether are irrelevant to their world view. In that world view, the SCC cannot be redeemed by reducing discount rates or even setting them to zero. Such discount-rate manipulation is simply an attempt to rig an economic model so that it produces a result pre-determined in the alternate world view.
For policymakers who find the SCC a useful tool, they must estimate it using a discount rate that reflects the greatest, reasonably expected return on alternative investments. Economic efficiency across time is not achieved by providing future benefits at too high a cost or by providing too few future benefits for a given cost.
A Hypothetical Climate Example
Suppose emitting a ton of CO2 today will cause $2,000 of damage (adjusted for inflation) in the year 2116. How much should be invested to prevent this emission?[6] In other words, how much should be invested today so that in 2116 the damage of the ton of CO2 is offset?
Assume the best alternative to cutting CO2 is a no-maintenance tree farm. Suppose further that $1.15 worth of seedlings will grow to $1,000 worth of trees in 100 years. In this example, the value of the trees grows at a 7 percent compound rate.
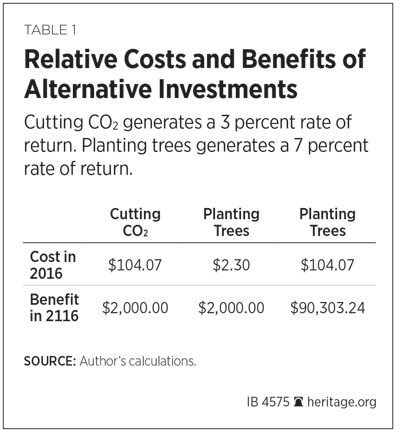
Discounting the $2,000 of CO2 damage for 100 years at 7 percent would give a present value of $2.30. That is, the SCC in 2016 is $2.30 (assuming, for simplicity, the damage is done only in 2116). In short, $2.30 worth of seedlings would create enough value in 2116 to offset the damage of the ton of CO2 emitted today. It would make little sense, then, to spend more than this for any other investment that produces only $2,000 of benefit in 2016.
However, that is just what some, including the EPA/IWG, recommend.[7]
Using the EPA/IWG’s too low 3 percent rate for discounting the climate damage gives a value of $104.07—roughly 50 times the value for the SCC obtained with the 7 percent discount rate. With this higher value as a guide, policies that cost $104.07 to cut CO2 emissions by one ton would pass muster, even though they provide no more benefit than planting $2.30 of seedlings.
Table 1 illustrates how the future is shortchanged if discounting is done with 3 percent when 7 percent returns would be available. The chart shows how a 3 percent discount rate equilibrates the present and future values when the cost of cutting CO2 is $104.07 per ton. With a 3 percent rate of return, $104.07 in 2016 would grow to $2,000 in 2116. However, if the current generation undertook projects with a 7 percent return rate, the return would grow to a value of more than $90,300.
What, then, is the best interest/discount rate to use?
Choosing the Right Discount Rate
Discounting is an opportunity cost exercise. The rate should reflect the best alternative return that an investment of the same size could reasonably be expected to generate.
What, then, is the best reasonable return on investment? While one cannot predict what future rates will be, past rates of return on broad indexes are an excellent guide. The return on the Standard & Poor’s 500 from 1928 to 2014 was 9.60 percent.[8] Over this time inflation was a compounded 3.1 percent. The real rate of return would be the difference—6.5 percent per year.
Another source estimates the return for all stocks in the U.S. from 1802 to 2002 and gets the same 6.5 percent real return on capital.[9] Yet another source calculates the real return on stocks between 1802 and 2002 to be 6.8 percent per year.[10]
These estimates reflect the returns after corporate income taxes are paid. Adjusting for corporate profits taxes increases these rates to between 7.5 percent and 9.9 percent. (See Appendix 2 for these calculations.) In any event, the 7 percent discount rate that is part the Office of Management and Budget’s guidance does not seem too high.
It is important to note that private investment differs in many ways from climate investment.
- The individuals making investments in climate improvement are not the same as those who receive the benefit of the investment.
- Climate improvement is a public good, which breaks the link between those who pay for the benefit and those who receive it.
- There are not well-developed markets for climate amenities that can give accurate valuations for the benefits and costs.
These differences may be problematic, but they are not problems with discount rates. As a result, they cannot be resolved by arbitrarily lowering the discount rate in a benefit-cost analysis.
Conclusion
Discounting is a critical component of cost-benefit analysis, especially when the costs and benefits occur at separate and temporally distant points. To be done properly, the discount rate should reflect the best rate of return that could reasonably be expected in capital markets. Over the past two centuries, the stock market in the U.S. has generated a return of more than 7 percent (after adjusting for the portion paid in taxes). Therefore, the 7 percent discount rate stipulated by the Office of Management and Budget for benefit-cost analysis seems very appropriate for use in analysis of climate policies.
—David W. Kreutzer, PhD, is Senior Research Fellow for Energy Economics and Climate Change in the Center for Data Analysis, of the Institute for Economic Freedom and Opportunity, at The Heritage Foundation.Appendix 1: Compounding and Discounting
Compound Interest
Most people are familiar with the concept of compound interest. For instance, if $100, the principal (present value or PV), were compounded at a 10 percent rate of interest, it would be worth $110 in one year. If none of the money were removed and the $110 were compounded for another year, the value at the end of this second year would be $121.00 (future value or FV).
The value at the end of the first year is $100 x (1+ 0.10) = $110. The interest rate is expressed as a decimal fraction, 0.10 = 10%.
The value at the end of the second year can be expressed as:
$110 x (1+0.10) = $121.
Another way of writing this is:
($100 x (1+0.10)) x (1+0.10) = $121; or $100 x (1+0.10)[2] = $121.
The general formula for compounded future value is:
FV=PV x (1+r)[n]
Where “r” is the rate of interest and “n” is the number of periods (typically years) over which the interest is compounded. In the example above PV = $100; r = 10 percent per year (written 0.10); and n = 2.
Present Value
Discounting is the inverse of compounding. For any amount in the future the present value (or discounted value) is the amount that, if invested today, would compound out to that future value. In the example above, the present value of $121 to be received two years from now discounted at 10 percent per year is $100. The general formula for compounding can be rearranged to give the general formula for discounting as:
PV=FV/(1+r)[n].
Appendix 2: Rates of Return
Taxing corporate profits transfers the taxed portion of these returns on capital to the government. Because of that transfer, this portion of the return to capital is not reflected in the standard rate of return estimates.
The average rate of return on the Standard & Poor’s from 1928 to 2014 was 6.5 percent. The average federal corporate profits tax for firms in the top income bracket (where most corporate profits are earned) from 1928 to 2014 was 38.3 percent. Not all profits are taxed at that rate nor does that rate include taxes at the state and local levels. The Bureau of Economic Analysis, however, did an in-depth study of the taxes paid by corporations in 1996.[11] Its numbers indicate an overall effective profits tax of 30.8 percent. In 1996 the statutory federal rate for corporations in the top bracket was 35 percent. Assuming that the same 4.2 differential between the federal rate and the effective overall tax rate holds in general puts the average corporate tax rate for 1928 to 2014 at 34.1 percent.
Therefore, the before-tax profits are larger than the after-tax profits by a factor of:
100 / (100 – 34.1) = 1.52.
That is, the rate of return to the country as a whole (as opposed to the return paid to stockholders) on the capital in the U.S. stock market for 1928–2014 was:
6.5 percent x 1.52 = 9.9 percent.
While there may have been other forms of corporate taxes before 1909, there was no federal corporate profits tax before that date. The average rate for the top profits bracket (which was not always the highest marginal tax rate) for the years 1909–2002 was 32.4 percent.[12] Subtracting 4.2 percentage points, to convert the federal nominal rate to an overall effective rate, yields 28.2 percent. Since the federal corporate profits tax was in effect for only 46 percent of the years between 1802 and 2002, the average corporate tax would be estimated by:
28.2 percent x 46 percent = 13 percent.
The adjustment factor for this time frame is:
100 / (100 – 13) = 1.15 percent.
Using the lower of the two estimates for the rate of return on all U.S. stocks from 1802–2002 gives a rate of return to the country as a whole of:
6.5 percent x 1.15=7.5 percent.
After including the value of corporate taxes, the return on stocks in the U.S. over long periods of time (1802–2002 in two cases and 1928–2014 in the other) range from 7.5 percent to 9.9 percent.
Appendix 3: The Logic (and Illogic) of Climate Investments
Some proponents of low discount rates argue that the forced investment in future climate amenities will come primarily at the expense of reduced consumption instead of alternative investment.[13] If this were true, then the cost of reduced consumption is even greater than the cost of reduced investment.
Why would people who consider a 7 percent return not worth sacrificing current consumption somehow think that a 3 percent return would be worth it?
Appeal to social-welfare functions and theoretical measures of how much additional income would be worth in the future, however, turn the argument on its head. Arguing that climate policies sacrifice current consumption instead of current investment is nonsensical with respect to basic economics. Sacrificing current consumption for greater future consumption is how all investment is done.
Requiring people to invest in future climate benefits by imposing climate regulations, but saying that it is unfair to compare that rate of return to rates from alternative investments, is tantamount to an investment advisor recommending a poorly performing fund. He may say it is illegitimate to compare the expected return to better investments because one is not saving for retirement in the first place. Yet who would want such advice? Anyone moving from not saving to saving will want the best return on the savings. In a similar vein, any investment for the future (whether voluntary or coerced) should be the one with the highest rate of return the investors could reasonably expect to earn. Biasing cost-benefit analysis so that investment is shunted to projects with lower rates of return is a poor strategy for helping those in the future.